* 본 포스팅은 주로 "다크프로그래머"님의 블로그를 기반으로 다른 여러 가지 문헌을 참조하여 작성되었음을 미리 알려드립니다.
본 포스팅에서는 핀홀 카메라 모델을 기반으로 월드 좌표계, 카메라 좌표계, 픽셀 좌표계, 그리고 정규 좌표계의 관계를 알아보도록 하겠습니다.
핀홀 카메라 모델 -> 카메라 모델
매칭관계: 핀홀-렌즈중심, 이미지가 맺히는 상자 내벽-이미지센서
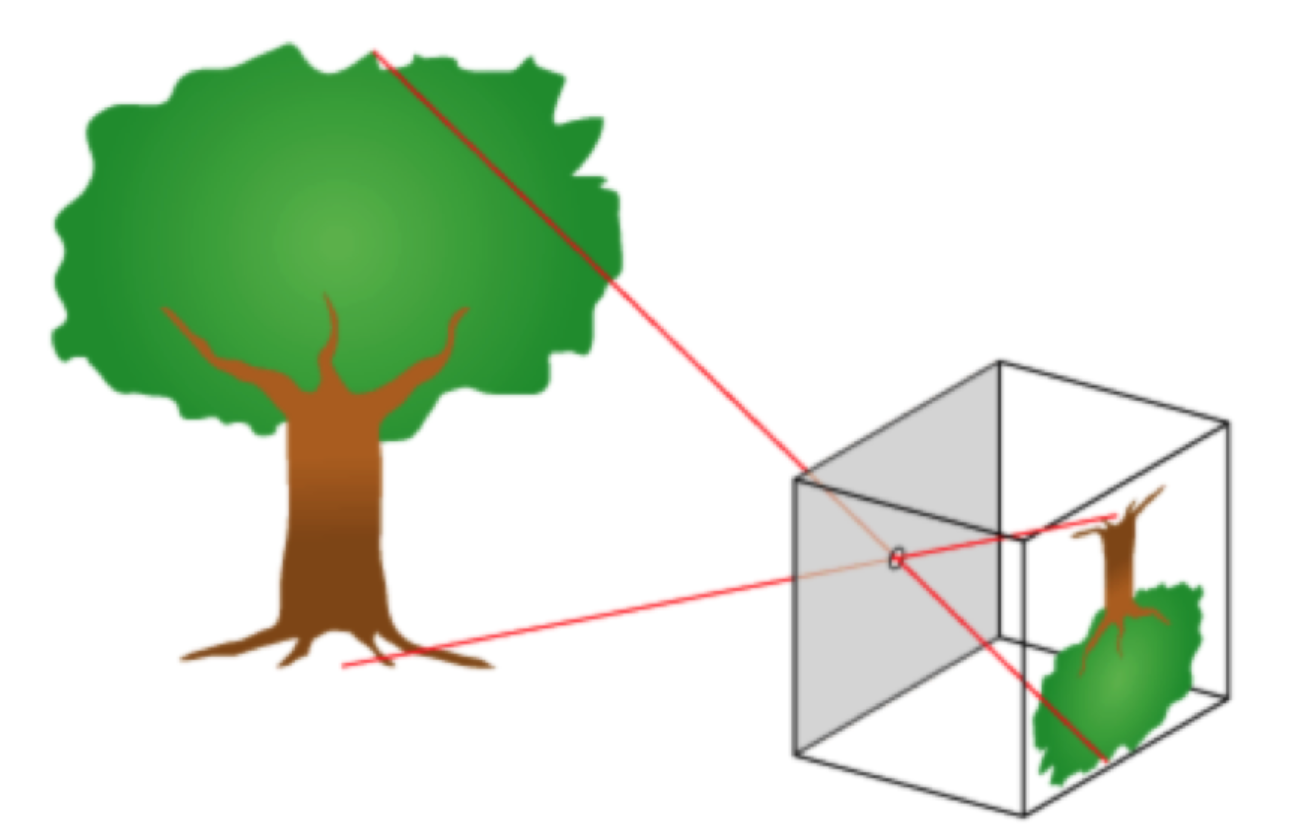

카메라 모델 표현 변경
그림 "카메라 모델 1"으로 표현하는 것이 정확하지만, 그림이 너무 크고 영상이 뒤집히는 것을 항상 생각해야 합니다.
좌표계의 변환 등 계산의 편의를 위해 그림 "카메라 모델 2" 처럼 Image sensor(Image plane)을 렌즈의 앞으로 옮겨서(실제로는 뒤에 있지만) 그림 "카메라 모델 3" 처럼 표현해봅시다.

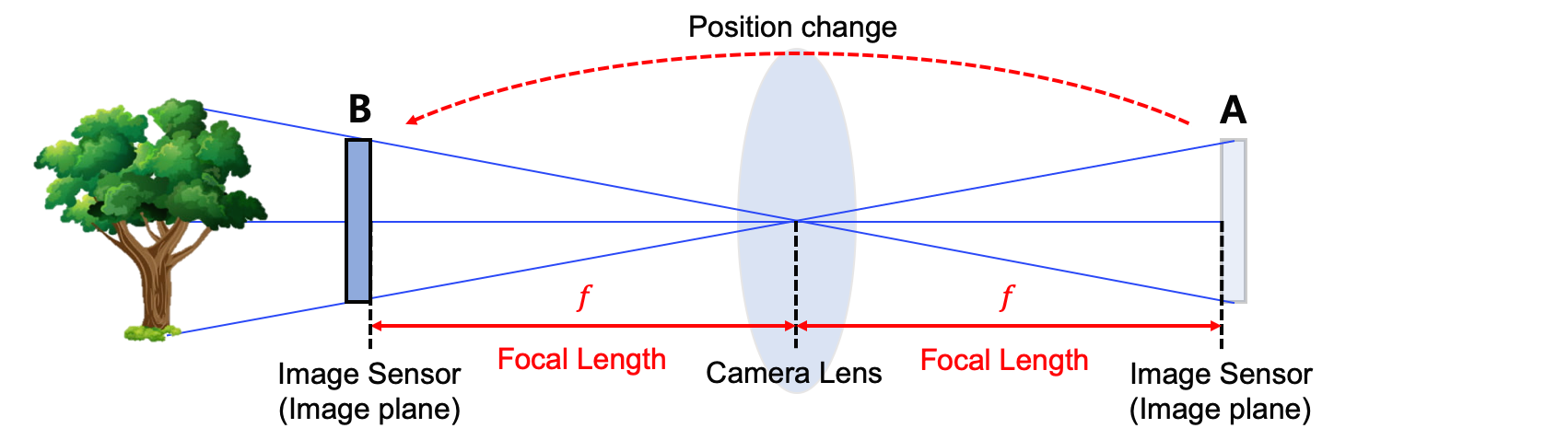

Zc는 피사체와 카메라(렌즈) 사이의 거리입니다.
픽셀 좌표계
Image sensor(Image plane)으로 좌표를 표현한 것
카메라 좌표계
Camera lens을 중심으로 좌표를 표현한 것
카메라의 세팅, 제조 과정의 차이로 인해 Focal length와 Principal point는 카메라마다 달라집니다. 그래서 우리는 동일한 피사체를 촬영하더라도 카메라에 따라 다른 이미지를 얻게 됩니다. 기하학적 해석을 할 때, 각각 다른 카메라의 특성에 따라 기하학적 해석을 하는 것은 굉장히 귀찮은 일입니다. 이러한 귀찮은 일을 하지 않기 위해, 어떤 카메라로 촬영하든 카메라 좌표계와 거리가 1이고, 중심의 좌표가 주점인 새로운 이미지 평면으로 좌표계(정규 좌표계)로 변환합니다. 즉, 우리는 정규 좌표계로 계산한 기하학적 해석만 있으면, 모든 카메라에 대한 기하학적 해석이 가능해집니다.

정규 좌표계
카메라 좌표계와 거리가 1이고, 중심의 좌표가 주점인 이미지 평면
편의상 도입된 좌표계
그림 "정규좌표계"에서, Image plane(픽셀 좌표계)에서 정규좌표계로 변환은 비례식을 이용하면 됩니다. 비례관계를 알기 위해서는 Focal length와 Principal point가 필요합니다. 즉, 픽셀 좌표계에서 정규 좌표계로 변환하기 위해서는 Intrinsic parameter가 필요합니다. 카메라의 Intrinsic parameter는 카메라마다 다르기 때문에 카메라마다 계산을 해주어야 하는데, Camera Calibration을 통해 얻을 수 있습니다. 픽셀 좌표계와 정규 좌표계의 변환 관계는 아래와 같습니다.
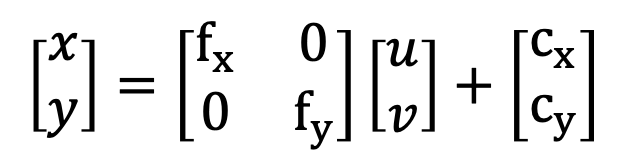
수식에 더하기가 들어가서 좀 복잡해 보입니다. 아래와 같이 차원을 하나 늘려서 더하기 항을 없애줍니다(Homogeneous representation).

P(u,v)는 정규 좌표계, P(x,y)는 픽셀 좌표계입니다.

지금까지 설명한 모든 좌표를 3D로 표현해보겠습니다.

그림에서 B, C, D는 위의 그림 "정규 좌표계"를 3D로 표현한 것입니다. 2D 그림과 3D로 표현한 그림을 잘 매칭해 보시길 바랍니다. 그리고 기준이 되는 월드좌표계를 3차원 그림에 추가하였습니다.
월드 좌표계
사물(물체)의 위치를 표현할 때, 기준으로 삼는 좌표계
실험실 구석, 로봇의 출발 위치 등 임의로 정하면 됨
월드 좌표계에서 카메라 좌표계로 변화하기 위해서는 3차원 회전, 3차원 이동이 필요합니다(다음 포스팅에서 좀 더 자세히 설명하도록 하겠습니다).

'Robotics > Vision' 카테고리의 다른 글
| [비전 #2] 카메라 모델 (Camera model: Intrinsic parameter) (0) | 2020.09.04 |
|---|---|
| [비전 #1] 핀홀 카메라 (Pinhole Camera): Focal length(초점거리) (0) | 2020.08.16 |
| [Feature extraction #1] SIFT 알고리즘 (0) | 2020.07.29 |

