2019. 9. 15 작성
2019. 9. 23 포스팅
2019. 9. 28 제어방법 추가
이전 포스팅에서는 State space representation에서 사용하는 기본적인 용어를 알아보았다. 이번 포스팅에서는 간단한 예제를 통해 동역학식을 어떻게 State space로 표현할 수 있는지에 대해 알아보고, Output feedback controller와 State feedback controller에 대해 간단히 알아볼 것이다.
State space representation of mass-spring system

위의 그림은 mass-spring system을 나타내는 그림이다. 마찰력이 없는 바퀴가 달려있고 무게가 m인 수레는 탄성계수가 k인 스프링에 의해 벽과 연결되어 있으며 Fa의 힘으로 오른쪽 방향으로 당겨지고 있다. 수레가 움직인 거리는 x로 나타내었다. mass-spring system의 dynamics(동역학식)는 다음과 같다.

위의 dynamics를 state space로 표현하면 다음과 같다.

그리고 외부힘 Fa를 제어입력 u로 생각한다.

위의 식을 행렬로 정리하여 State Space Representation으로 나타낸다.


우리는 현재의 위치 및 속도 등의 상태(x1, x2)와 시스템의 모델(A, B)을 알고 있으면, 적절한 제어입력을 선택하여 다음 상태의 속도와 가속도(x1_dot, x2_dot)를 결정할 수 있다. 즉, 제어입력 u를 잘 선택하면 위의 mass-spring system에서의 수레의 속도 및 가속도를 결정하여 수레를 원하는 위치로 이동시킬 수 있다는 것이다. <수레(시스템)를 원하는 위치에 가져다 놓는 것> 이것을 우리는 수레(시스템)의 위치를 제어한다고 말한다.
시스템을 제어하기 위해서는 제어입력 u를 시스템의 제어 주기에 맞춰 넣어주면 된다. 예를 들어, 에어컨처럼 천천히 제어해도 되는 시스템은 10초마다 현재의 온도에 따라 제어 입력 u를 시스템에 줄 것이고, 무인자동차처럼 빠르게 제어되어야 하는 시스템의 경우 0.03초마다 현재의 위치와 속도에 따라 제어 입력 u를 시스템에 줄 것이다(여기서 제시한 숫자는 정확하지 않음). 즉, 매 제어주기마다 원하는 위치와 현재의 상태를 기반으로 제어 입력 u를 결정하여 시스템에 넣어주는 것이다. 제어 입력 u는 시스템이 빠르고 정확하게 원하는 위치에 도달하도록 결정하는 것이 좋을 것이다. 그렇다면 어떻게 빠르고 정확하게 원하는 위치에 시스템이 도달하도록 제어 입력 u를 결정할 수 있을까?
Output feedback control vs State feedback control
시스템이 빠르고 정확하게 원하는 위치하도록 하는 제어 방법은 크게 Output feedback control과 State feedback control 이 있다.
1. Output feedback control
Output feedback control은 현재의 상태를 센서로 측정하고, 이를 되먹임(feedback)하여 제어하는 방법이다. 우리가 가장 많이 사용하는 PID controller가 Output feedback controller에 해당한다.

센서에서 측정한 현재의 상태 y(t)와 원하는 위치 r(t)와의 차이 e(t)와 e(t)를 적분 및 미분한 값에 각각 Kp, Ki, 그리고 Kd의 PID 게인을 곱하여 제어 입력으로 사용하는 방법이다. 위의 수식에서 표현된 것처럼 Output feedback control은 시스템의 모델(A, B) 없이 제어할 수 있는 장점이 있다. 시스템이 원하는 위치에 도달하면 r(t) = y(t) 이기 때문에 e(t) = 0 이 되고, 제어 입력 u(t) = 0 [e(t) = 0, 미분(e(t)) = 0, 적분(e(t)) = 0] 이 되기 때문에 시스템은 움직이지 않는다(적분항에 의한 누적에러는 여기서 고려하지 않았다). PID controller의 performance는 PID 게인 (Kp, Ki, Kd)을 어떻게 설정하는가에 따라 크게 달라진다. 여러 가지 방법들이 있지만 보통 trial and error (시행착오 -> 노가다ㅠㅠ)를 통해 구한다.
2. State feedback control
State feedback control은 말 그대로 시스템의 상태를 되먹임(feedback)하여 제어하는 방법이다.

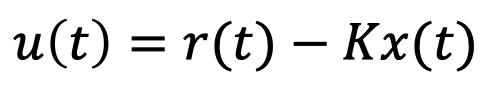
문제를 단순화하기 위해서 위치, 속도 등 우리가 원하는 상태가 모두 r(t) = 0이라고 가정하면, 제어 입력 u(t)는 다음과 같다.

State feedback control은 Output feedback control과 달리 시스템의 모델(A, B)을 알아야 한다. State feedback control input을 시스템의 dynamics에 대입하면 다음과 같다.

시스템 모델(A, B)는 변하지 않는 값이기 때문에, 우리는 K를 적절히 결정해서 시스템이 어떤 속도와 가속도로 움직여야 할지 조절할 수 있다. State feedback control의 performance는 Output feedback control의 PID 게인을 어떻게 조절하는지에 따라 달라진 것처럼, K를 어떻게 조절하는지에 따라 결정된다. 하지만, Output feedback control과 비교되는 가장 큰 장점은 trial and error 방법을 이용해 K를 구하는 것이 아니라, 시스템 모델(A, B)을 이용해서 K를 결정할 수 있다는 점이다. 즉, 모델만 정확하다면 optimal 한 K를 계산할 수 있어서 게인 값을 찾는데 드는 시간을 줄일 수 있다(게인 값을 시행착오 법으로 찾는 것은 많은 시간, 노력, 노하우가 필요하다).
그럼 State feedback control에서 K는 어떻게 계산할 수 있을까? 이에 대한 내용은 다음 포스팅에서 이어하도록 하겠다.

'Robotics > 제어' 카테고리의 다른 글
| LQR제어 - ARE (Algebraic Riccati Equation) (6) | 2019.12.21 |
|---|---|
| LQR제어 - Lyapunov Function (리아프노브 함수) (11) | 2019.10.15 |
| LQR제어 - State Space Representation (상태방정식) (0) | 2019.03.14 |
| 보드선도(bode plot)_2 (4) | 2019.01.05 |
| 보드선도(bode plot)_1 (0) | 2019.01.05 |