2019. 10. 4 작성
2019. 10. 11 추가 작성
2019. 10. 15 포스팅
2019. 10. xx ARE에 대해 작성 중
2021. 12. 13 Q: negative definite --> -Q: negative definite 로 수정
이전 포스팅에서는 Mass-spring system의 state space representation과 시스템의 제어방법에 대해 알아보았습니다. 제어 방법으로 Output feedback control과 State feedback control 에 대해 알아보았고, 두 제어방법의 차이에 대해서도 알아보았습니다. 두 제어방법은 각각의 장점과 단점이 있기 때문에 우열을 가리는 것은 어렵지만 본 [LQR series]에서는 LQR control을 설명하고자 하기 때문에 State feedback control을 기반으로 설명하도록 하겠습니다.

State feedback control의 장점은 모델만 정확하다면 optimal한 K를 계산할 수 있어서 게인 값을 찾는데 드는 시간을 줄일 수 있다는 것입니다. 그럼 State feedback control에서 K는 어떻게 계산할 수 있을까요? 본 포스팅에서는 optimal value를 구하는데 사용하는 Lyapunov function에 대해 알아보도록 하겠습니다.
System의 Stability를 판정하는 방법
시스템의 stability를 판정하는 방법은 다음과 같습니다.
1. Solution, State transition matrix를 구해서 stability를 판별하는 방법
- Linear dynamical system의 general solution을 구하는데 사용.
2. Eigenvalue check
- System의 eigenvalue가 positive real part에 있으면 unstable, nagative real part에 있으면 stable.
3. Lyapunov function
- Loss function의 미분값이 음수(-)가 되도록 설계하여 항상 Loss function의 최소값을 구하는 방법
System이 주어지면 이미 solution이 define되어 있기 때문에, 모든 solution을 그리면 시스템이 stable한지 판별할 수 있습니다. 하지만 모든 solution을 구하는 것은 너무 비효율적입니다. Lyapunov function은 solution을 구하지 않고 안정도를 판별할 수 있는 방법입니다.
Lyapunov Stability
다음은 등고선그림 및 등고선 함수를 나타낸 것입니다.


산속에서 길을 잃었을 때, 산 아래로 내려가는 가장 직관적인 방법은 내리막길로 이동하는 것입니다. 이와 마찬가지로, 줄이려고 하는 값(error 등)을 변수로 하는 Loss function을 만들고 그 미분값이 항상 음수(-)가 되도록 설계하면 시간이 지날수록 Loss function은 최소값에 도달하게 될 것입니다. 즉, 모든 x에 대해서 등고선 함수의 미분값 V_dot(x) < 0 (단, x!=0)을 보일 수 있다면, 초기값이 어디에 위치하든 Loss function이 최소가 되는 게인값 K를 찾을 수 있습니다.
Lyapunov Function
이제부터 Lyapunov function이 수식으로 어떻게 나타나는지 알아보도록 하겠습니다. 다음과 같은 시스템을 제어한다고 가정합니다.

Loss function 을 다음과 같이 정의합니다.

transpose(x)는 fat 행렬(가로로 긴 행렬), P는 정방행렬, 그리고 x는 tall 행렬(세로로 긴 행렬)입니다. 그리고 P 행렬은 positive definite (matrix) [1-2]입니다. 즉, non-zero colume vecotr x와 transpose(x) 사이에 positive definite P를 multiplication(행렬곱)하면 오목한 모양[2]의 그래프를 얻을 수 있는데, V(x)를 오목한 모양이 되도록 설계합니다. 그럼 설계한 V(x)를 x로 미분합니다.

우리는 V_dot(x) < 0 으로 만들기 위해서는 V_dot(x)를 다음과 같이 설계하면 됩니다.


A는 시스템의 모델이기 때문에 이미 주어져 있습니다. 따라서 Lyapunov equation -Q가 negative definite가 되도록 적절한 P (positive definite)를 설정하면 시간이 지날수록 V(x)의 값이 줄어들도록 할 수 있습니다(항상 0으로 수렴하는 것은 아니지만, 0으로 수렴할 가능성도 가지고 있습니다).

여기서 우리는 V(x)를 "Lyapunov function" 이라고 합니다.
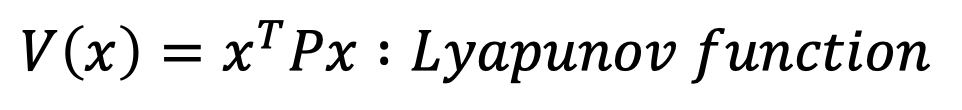
마지막으로 어떻게 positive definite P를 구하는지 알아보는 일만 남았습니다.
Algebraic Riccati Equation (ARE)
다음 포스팅에서는 ARE를 증명하는 방법을 알아볼 예정입니다. 여기에서는 positive definite P를 계산하는 ARE와 최적의 게인값인 K를 계산하는 방법을 소개하도록 하겠습니다. 이해가 되지 않으시면 그냥 넘어가셔도 좋습니다. 다음 포스팅에서 좀 더 자세하게 설명하도록 하겠습니다. (단, Q와 R은 시스템의 상태와 제어입력 중 어느것을 상대적으로 더 줄일지에 따라 사용자가 결정하는 상수값입니다.)
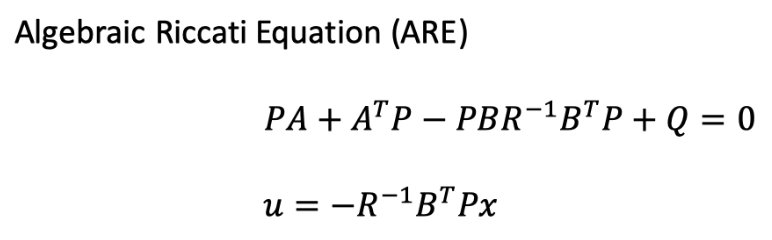
[1] https://en.wikipedia.org/wiki/Definiteness_of_a_matrix

'Robotics > 제어' 카테고리의 다른 글
| Autonomous System (자율 주행을 위한 반드시 필요한 4가지 절차) (0) | 2021.04.11 |
|---|---|
| LQR제어 - ARE (Algebraic Riccati Equation) (6) | 2019.12.21 |
| LQR제어 - State Space Representation and Control for Mass-spring system (2) | 2019.09.23 |
| LQR제어 - State Space Representation (상태방정식) (0) | 2019.03.14 |
| 보드선도(bode plot)_2 (4) | 2019.01.05 |
